1 引言

本章简介

本章主要介绍精算学的基本概念、发展历史、职业特点、考试体系和基本原理。精算学的发展历史可以追溯到17世纪，随着保险行业的发展，精算学逐渐成为保险行业的核心技术之一。精算师是从事精算工作的专业人员，主要负责保险产品的定价、风险评估、资产负债管理等工作。精算师考试是成为一名精算师的必经之路。最后用一个简单例子来介绍精算学的基本原理。

学习目标

  1. 了解精算学的基本概念和发展历史；
  2. 了解精算职业特点与精算管理控制系统；
  3. 了解精算考试体系及其科目设置；
  4. 熟悉精算原理及其基本应用。

1.1 精算学发展简史6

精算学为保险行业提供了科学可靠的解决方法，不断推动保险行业的健康发展；同时保险行业也为精算学提出了更高的要求，成为精算学发展的行业动力。

1.1.1 精算学的基础

概率论是精算学的数学基石。1648年，费马（Fermat）和帕斯卡（Pascal）关于赌博问题的通信，开启了概率论发展的脉络 ，他们在解决问题时采用先验概率（即频率学派）。之后，根据数据来估计概率并应用于实际的思想逐渐被接受，概率论的应用领域得以拓展，精算学便是其中之一。

18世纪早期，精算学的发展推动了概率论成为统计学的基础，埃德蒙·哈雷（Edmund Halley）、雅各布·伯努利（Jacob Bernoulli）和亚伯拉罕·棣莫弗（Abraham De Moivre）等对此做出了重要贡献。哈雷于1693年发表了布雷斯劳表（Breslau Table），其生命表格式沿用至今；伯努利在其著作《猜度术》（Ars Conjectandi）中提出大数定律，为精算师和其他应用科学家使用概率论的相对频率估计解决实际问题提供了依据；棣莫弗的贡献涉及精算学理论构建和基础建设，他的《人寿年金》包含诸多原创思想 ，其在证明二项分布趋近正态分布方面的工作也意义重大。

商业实践是精算学的行业基础。1545年，英国允许贷款收取利息。1540年，荷兰数学家杰玛·弗里苏斯（Gemma Frisus）在一本教科书中总结了这种情况，解释了复利的用处。1582年，西蒙·斯蒂文（Simon Stevin）出版了现值表，该表的年利率为116%、投资期限为130年。

效用理论则成为是精算学发展中的经济理论基础。丹尼尔·伯努利（Daniel Bernoulli）关于货币 “道德价值”的研究中指出，期望值在描述人们面对不确定性时的决策存在缺陷，提出了边际效用递减概念，并构建对数效用函数，证明决策者会为保险支付高于损失期望值的费用，这成为保险行业的理论基础。但这一思想在20世纪后半叶才对精算学产生重大影响。

1.1.2 精算学在保险行业的初步应用

概率论与复利理论的结合催生了精算学，并首次应用于年金领域。1671年，荷兰首相约翰·德维特（John De Witt）基于可能受观测影响的生命表和复利表计算年金价值 。哈雷在论文中也计算了年金价值。棣莫弗综合前人工作，撰写了关于人寿年金的教科书。

1743年成立的苏格兰部长遗孀基金（Scottish Ministers Widows Fund）是首个具有明确福利、资金计划和财务运营预测的养老金计划，其主要设计者为罗伯特·华莱士（Robert Wallace）和亚历山大·韦伯斯特（Alexander Webster），数学家科林·麦克劳林（Colin Maclaurin）也做出了贡献。

1762年，伦敦成立了公平人寿保险社（Society for Equitable Assurance on Lives and Survivorships），基于科学原则开展人寿保险业务，其创始人詹姆斯·多德森（James Dodson）提出人寿保险保费应终身固定但随参保年龄变化的理念。1775年，公平人寿保险社的精算师威廉·摩根（William Morgan）对公司进行首次估值，发现实际死亡率低于预期 ，随后公司采用北安普敦表（Northampton Table）作为保费和估值的基础。理查德·普赖斯（Richard Price）对精算学贡献巨大，他的教科书在19世纪一直是人寿保险数学的主要教材，还因发表托马斯·贝叶斯（Thomas Bayes）的论文而闻名。

1.1.3 精算学研究范畴的逐步拓展

19世纪，保险行业迅速扩张，精算师专业组织开始出现，精算实践的科学基础不断发展。大数定律被广泛用于计算长期合同的保费和准备金、短期保险的预期索赔数量和金额，但在应用中仍然缺乏必要的理论支撑和技术解释。

为了应对这一问题，风险理论逐步兴起，其中为人所熟知的成果通常称为个体风险理论（Individual Risk Theory）。该理论研究多个独立同分布风险单位的期望偏差，计算期望、方差及相关分布，常借助中心极限定理来使用正态分布。

精算学与人口学紧密相关，18-19世纪，两者在死亡率数据收集分析、生命表构建和修匀（graduation）方面共同发展。随后，许多国家逐步开展定期人口普查，有些国家则开展连续性人口登记，这些都为精算研究提供了数据支持。

1.1.4 随机过程与精算学的融合

20世纪初，随机过程研究蓬勃发展。爱因斯坦（Einstein）解释了布朗运动，巴舍利耶（Bachelier）在博士论文中对投机价格建模，其思想在20世纪最后30年对精算学产生了巨大影响。20世纪30年代，瑞典人菲利普·伦德伯格（Filip Lundberg）提出集体风险理论（Collective Risk Theory），该理论将保险业务视为一个整体，而非关注单个保单。该理论基本模型涉及索赔总额、索赔金额和索赔频率等随机变量 ，并提出破产理论（Ruin Theory ）作为保险过程稳定性的标准。 此外，贝叶斯方法在精算学中的应用逐渐发展起来，20世纪40年代开始基于贝叶斯方法的可信度理论（Credibility）得到全面发展。

20世纪40年代电子计算机出现后，其在保险行业的应用改变了精算学。计算机模拟成为解决聚合索赔分布问题的实用方法，还用于模拟更复杂的模型。计算机对保险产品设计也产生了深远影响，推动了万能保险和变额保险产品的发展。

20世纪后半叶，多状态随机过程在精算实践中得到应用，用于为长期护理保险和持续护理退休社区等金融安全系统建模。金融经济学的研究成果，如免疫理论、投资组合理论、有效市场假说、资本资产定价模型和期权定价理论等，也对精算学产生了重要影响，并逐渐融入精算研究和实践中。

1.2 精算师职业

精算师（Actuary）是保险公司、金融机构、政府部门等单位中从事精算工作的专业人员。精算师的主要工作是利用数学、统计学、金融学等知识，在产品定价、风险评估、资产负债管理等方面为所在机构提供专业判断和建议，以保障所在机构的经营安全。

1.2.1 精算师工作领域

精算师的工作领域非常广泛，主要包括保险公司、金融机构、政府部门等。在保险公司，精算师主要负责保险产品的定价、风险评估、资产负债管理等工作；在金融机构，精算师主要负责金融产品的定价、风险评估、资产负债管理等工作；在政府部门，精算师主要负责社会保障、养老金、医疗保险等公共保险项目的设计、评估、监督等工作。

精算师在保险行业的工作内容主要包括以下五个方面：

  1. 保险产品的定价：精算师通过对保险产品的风险评估、损失预测、费率设计等工作，确定保险产品的定价，保障保险公司的经营安全。

  2. 资产负债管理：精算师通过对保险公司的资产负债情况进行分析、评估、管理，保障保险公司的资产负债平衡，降低经营风险。

  3. 风险评估：精算师通过对保险产品的风险评估、损失预测、风险管理等工作，评估保险公司的风险水平，降低经营风险。

  4. 产品设计：精算师通过对保险产品的需求分析、市场调研、产品设计等工作，设计出符合市场需求、风险可控的保险产品。

  5. 数据分析：精算师通过对保险产品的数据进行分析、建模、预测等工作，为保险公司的经营决策提供数据支持。

1.2.2 精算管理控制系统

由于各种保险类型的不同特点，在实践中形成了分别用于寿险、非寿险、养老金、投资、社会保障、再保险等不同领域相对独立的精算体系。这些体系的形成和发展对镜算技术的专门化具有重要作用，但也对精算工作领域的扩展产生了一定的限制作用。

1985年，英国精算师杰里米·戈福德（Jeremy Goford）提出了精算管理控制系统（Actuarial Control Cycle）的概念，强调精算在保险公司管理各个环节中的作用及相互联系，具体内容参见1.1。

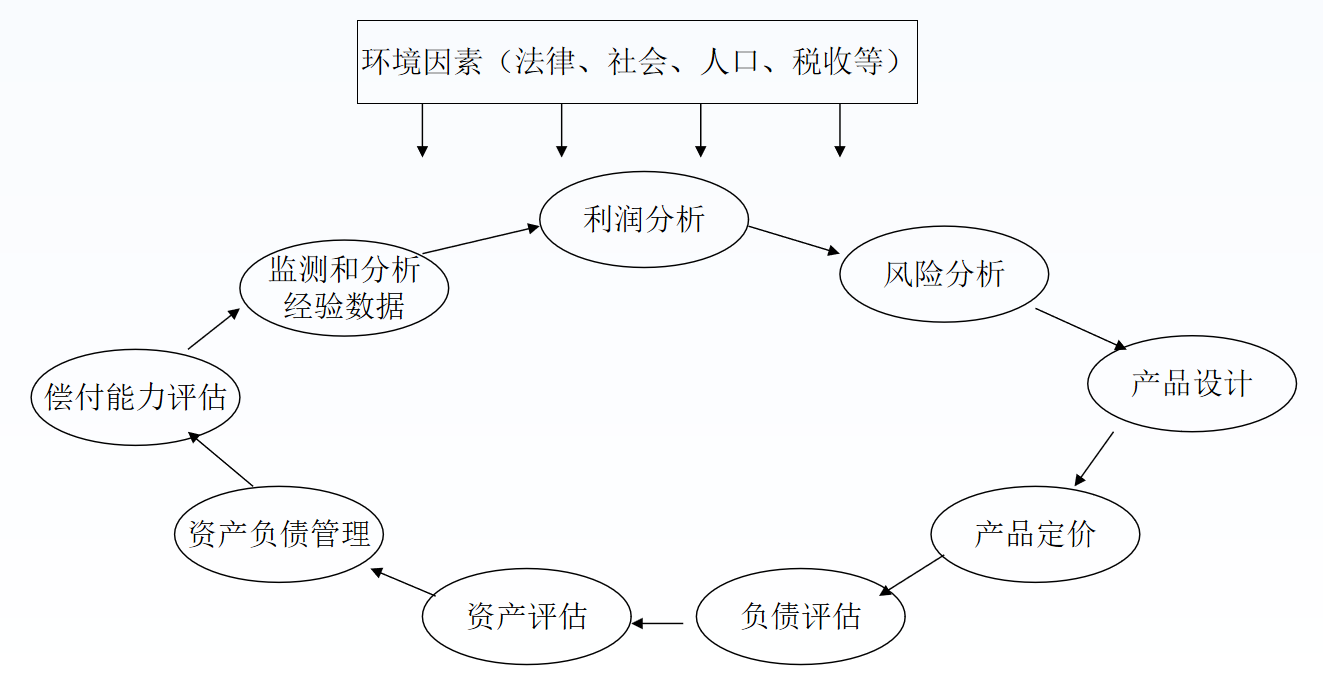
精算管理控制系统示意图

图1.1: 精算管理控制系统示意图

1.3 精算师考试

由于精算职业对保险行业发展的重要程度，如果一个人要成为一名精算师必须经过严格的专业培训和考试，同时保险公司经营必须要聘用经认可的精算专业人员。《中华人民共和国保险法》第八十五条明确规定：保险公司应当聘用专业人员，建立精算报告制度和合规报告制度。目前比较知名的精算师考试包括SoA、中国精算师考试等。

1.3.1 SoA精算师考试

北美精算师协会（Society of Actuaries，SoA）是全球最大的精算师协会之一，成立于1949年，总部位于美国伊利诺伊州斯科基。SoA的宗旨是促进精算学的发展，提高精算师的专业水平，保障公众利益。作为世界最为知名的精算考试之一，SoA考试科目涵盖范围较广。以SOA准精算师（Associate of the Society of Actuaries, ASA）为例，其考试课程7（截至2024年）如下：

考试科目 内容概要
Exam P: Probability 概率论与数理统计（概率模型、随机变量、贝叶斯定理等）
Exam FM: Financial Mathematics 金融数学（货币时间价值、年金、债券定价、久期与凸性）
Exam FAM: Fundamentals of Actuarial Mathematics 寿险/年金与金融衍生品（整合原MLC和MFE内容）
Exam SRM: Statistics for Risk Modeling 风险建模统计学（回归分析、时间序列、机器学习基础）
Exam PA: Predictive Analytics 预测分析实战（数据清洗、R/Python建模、模型解释）

1.3.2 中国精算师考试

中国精算师考试由中国保险行业协会主办，是中国保险行业的专业资格考试。中国精算师职业资格考试设置准精算师和正精算师两个级别。准精算师级别考试包括《概率论与数理统计》、《经济金融综合》、《精算数学》、《精算模型与数据分析》、《精算风险管理》5门科目。正精算师级别考试分为寿险、非寿险、健康险、社会保险与养老金计划、金融风险管理、资产管理、数据科学7个专业类别，每个专业类别包括1门公共科目、3门专业科目、1门选考科目。

以“准精算师”考试为例，其考试科目8如下：

考试科目 考试要求
概率论与数理统计 应掌握基本的概率统计知识，了解基本概率分布、统计量的性质，具备一定的求解概率和解决估计、检验等统计问题的能力。
经济金融综合 应掌握现代微观经济学、宏观经济学、金融学、保险学、会计与财务的基本概念、基本方法和原理，掌握和运用经济金融学中的主要定性分析和定量分析方法，具备较宽的专业知识面和较强的分析问题、解决问题的能力。
精算数学 应掌握复利数学、寿险精算、非寿险精算的基本概念、理论和方法，理解精算学中的基本原理和概念，具有熟练的精算计算能力。
精算模型与数据分析 应掌握精算模型的基本理论和方法，能够对保险经营中的损失风险和经营风险进行定量分析；掌握生存模型理论、生命表基础知识及生存函数的估计，了解生命表编制原理；掌握随机模拟、回归分析、时间序列的基础原理、方法和应用；了解机器学习的基本原理，具备对数据进行分析的能力。
精算风险管理 应掌握风险管理的基本概念、框架和流程，能够对业务和环境中的风险进行正确地识别和分类；能够利用金融、统计、精算技术对不同风险进行建模、度量、评估，对风险之间的相关性、风险聚合等进行量化分析；能够利用恰当的风险管理工具和技术进行有效的风险管理；理解经济资本、偿付能力的概念，掌握运用经济资本进行风险管理的原理和方法，熟悉我国偿付能力监管体系。

1.4 精算原理概述

回到序中那个例子：

张三现年30岁，购买了一份一年期寿险（保险责任为身故、按标准体承保），保额10万。那么产品参数及其业务要求如下设定：

  • x：投保年龄(x=30)
  • n：保险期限为1年(n=1)
  • b：保险金额(b=10)
  • \(q_x\): 张三1年内的死亡率(假定\(q_x\)=1‰)

按照概率论原理和保险合同约定，1年内保险公司对保险受益人的或有赔付及其概率可以表示如下：

事件 张三在1年内发生身故 张三在1年内始终生存
保险公司的可能赔付（万元） 10 0
概率（‰） 1 999

按照收支对等（公平保费）原则，即保险公司应收取的保费应该等于保险公司的期望赔付，在不考虑保险公司的利息、费用、投资收益、利润的情况下：

保费=期望损失=100,000×1‰ + 0×999‰=100元

例1.1 某博物馆为其100件馆藏文物投保了1年期定值保险，合同约定如果投保文物在保险期间出险，保险公司固定赔付5万元。已知每件文物在保险期间内发生损失的概率为1%，且文物之间风险独立。如果不考虑费用、投资收益、利润的情况下，请计算文物的公平保费。

解. 每件文物的公平保费=50,000×1% = 500元。

因此，100件文物的公平保费=100×500=50,000元。

1.5 课后习题

  1. 简述精算学的基本概念和发展历史。
  2. 简述精算师的职业特点和精算管理控制系统。
  3. 简述中国精算师考试的科目设置。
  4. 简要分析概率论中“大数法则”与保险精算中“公平保费”之间的关系。

References

Teugels, Jozef L., and Bjørn Sundt, eds. 2004. Encyclopedia of Actuarial Science. 1st ed. Wiley. https://doi.org/10.1002/9780470012505.

  1. 本节内容参考了(Teugels and Sundt 2004)中的“History of Actuarial Science”条目。↩︎

  2. 参见网址：https://www.soa.org/education/exam-req/edu-asa-req.aspx。↩︎

  3. 参见网址：https://www.e-caa.org.cn/actuarialExams/11。↩︎