2 利息理论

内容简介

在日常经济生活中，利息或利率是倍受关注的经济变量。无论个人还是企业，利率水平的高低直接影响着他们的消费行为和投资策略。可以毫不夸张地说，利率问题是金融市场最基础、最核心的问题之一，几乎所有的金融现象都与利率有着或多或少的联系。因此我们首先介绍有关利息和利率的度量，主要包括实际利率、名义利率、利息力等重要的概念及其数量关系。在此基础上我们还讨论了年金，即一系列有规律的现金流的现值与终值的计算公式及其相关关系。

学习目标

  • 理解资金累积生息过程，掌握实际利率的计算方法；
  • 掌握复利与单利的计算及其与实际利率之间的关系；
  • 掌握名义利率与实际利率之间的换算关系；
  • 掌握利息力的含义及其计算；
  • 掌握定期年金的现值和终值计算；
  • 了解久期、凸性等利率风险度量方法。

施振荣1944年生于台湾彰化县，父亲在他3岁时去世，留下他和母亲相依为命。为了将儿子抚养成人，施振荣的母亲做过各种小生意。在施振荣10岁时，母亲开了一家小卖店，同时出售鸭蛋和文具。当时，鸭蛋3元1斤，每斤赚3角，只有10%的利润。更主要的是，鸭蛋不易储存，很容易变质；而文具的利润高，如果做10元的生意，一下子便可以赚4元，利润高达40%。而卖文具还有一大好处，便是摆着不会变坏。看起来，卖文具比卖鸭蛋赚钱。不过在当时，卖鸭蛋却比卖文具要赚得多很多，为什么呢？

年纪小小的施振荣对这种情况进行了仔细的观察，最终他发现：鸭蛋利润薄，但最多两天周转一次；文具利润高，可有时一年甚至半年都卖不掉，不但积压成本，而且利润更早被利息吃光了。鸭蛋虽然利薄，但是多销，所以，利润大于周转缓慢的文具。

—资料来源：卖鸭蛋还是卖文具

2.1 利息基本理论

例2.1 资金累积生息过程

某年年初张三将1000元借给李四，一年后李四按照约定，不仅偿还了1000元而且还额外给甲50元作为利息，因此乙偿还的金额总计1050元。

在上述过程中，可以做如下定义：

定义2.1 本金：资金借贷业务开始时的金额（即1000元）。

定义2.2 累积值：又称为“本息和、终值”，在一定时间（1年）后回收的总金额（即1050元）。

定义2.3 利息：累积值与本金之间的差额（即50元）

定义2.4 利率：利息与本金之比，通常以百分数表示。同时，利率还要考虑时间因素，一般而言利率通常以年为单位。

在例2.1中，因为借贷时间恰好为一年，将利息（50元）和本金（1000元）带入可得，这次借贷的年利率为5%。

在上述定义的基础上，我们将资金累积过程进行数学化处理，一般化地描述资金借贷或投资行为。

2.1.1 累积函数与实际利率

累积函数是指期初1元本金在时刻t时的累积值，记为\(a(t)\)。\(a(t)\)具有下述性质：

  • \(a(t)\)是关于时间t的函数，\(a(0)\)为本金且恒等于1；
  • 当利率大于零，则累积函数\(a(t)\)为递增函数。反之，当出现投资失败即利率小于零的情况时，累积函数\(a(t)\)则为递减函数。
  • 如果连续结转利息，则累积函数\(a(t)\)为连续函数；反之，如果间断结转利息，则累积函数\(a(t)\)为非连续函数；
  • 当本金不是1元，而是金额\(A(0)\)时，则在时刻t的累积值为\(A(t) = A(0)×a(t)\)，相对应地，\(a(t)=\frac{A(t)}{A(0)}\) 。由此可见，A(t)和a(t)可以互相表示；
  • 若以\(I(t)\)表示0～t时期的利息额，则有\(I(t) = A(t)－A(0)=A(0)\times\left[a(t)-1\right]\)。

定义2.5 实际利率用来衡量累计过程\(a(t)\)在单位时间内（如第t年）资金生息水平，计算公式为：

\[\begin{equation} i_t=\frac{a(t)-a(t-1)}{a(t-1)} \tag{2.1} \end{equation}\]

例2.2 实际利率计算

某累积函数为\(a(t)=1.05^t+0.08\times\sqrt{t}\)，求第1年、第3年和第10年的实际利率。

解. 第1年的实际利率为：\(i_1=\frac{a(1)-a(0)}{a(0)}=\frac{1.13-1}{1}=13\%\)

第3年的实际利率为：\(i_3=\frac{a(3)-a(2)}{a(2)}=\frac{1.05^3+0.08\times\sqrt{3}-1.05^2-0.08\times\sqrt{2}}{1.05^2+0.08\times\sqrt{2}}\approx 6.63\%\)

第10年的实际利率为：\(i_{10}=\frac{a(10)-a(9)}{a(9)}=\frac{1.05^{10}+0.08\times\sqrt{10}-1.05^9-0.08\times\sqrt{9}}{1.05^9+0.08\times\sqrt{9}}\approx 5.05\%\)

2.1.2 贴现函数与实际贴现率

根据累积函数的定义，1元本金经过时期t后累积值为\(a(t)\)。如果将该问题换一个角度思考，即在时刻t后会得到1元的累积值，那么其对应的期初本金应该是多少？这一过程可以理解为将终值换算成现值的过程，一般称为贴现过程。

如果在t期末希望获得1元累积值，期初的本金就应该是\(a^{–1}(t)=\frac{1}{a(t)}\)，则\(a^{–1}(t)\)被称为贴现函数。

定义2.6 实际贴现率是指一定时期内的利息与期末累积值的比率，计算公式为：

\[\begin{equation} d_t=\frac{a(t)-a(t-1)}{a(t)} \tag{2.2} \end{equation}\]

例2.3 试证明：在单位时间内，实际利率i与实际贴现率d的关系可以描述为

\[\begin{equation} d=\frac{i}{1+i} \tag{2.3} \end{equation}\] \[\begin{equation} i=\frac{d}{1-d}\tag{2.4} \end{equation}\]

2.1.3 单利与复利

在实际生活中，最为常见的累积函数形式是单利和复利。单利是指在一定时期内，只给本金计息而对以前已经产生的利息不再计息。复利则是指在一定时期内，本金和前期产生的利息均计息。

单利累积函数为：

\[\begin{equation} a(t)=1+i\times t \tag{2.5} \end{equation}\]

复利累积函数为：

\[\begin{equation} a(t)=(1+i)^t \tag{2.6} \end{equation}\]

例2.4 单利条件下，对应的贴现函数为\(a^{-1}(t)=\frac{1}{1+i\times t}\)

第t年的实际利率为

\[i_t=\frac{a(t)-a(t-1)}{a(t-1)}=\frac{i}{1+i\times (t-1)}\]

显然：

\[ \lim_{t\to\infty}i_t=\lim_{t\to\infty}\frac{i}{1+i\times t}=0 \]

其经济含义为单利条件下的实际利率是随着时间t的增加而递减。

例2.5 复利条件下，对应的贴现函数为\(a^{-1}(t)=(1+i)^{-t}\)。定义\(v=\frac{1}{1+i}\)为贴现因子。

第t年的实际利率为

\[ \begin{aligned} i_t&=\frac{a(t)-a(t-1)}{a(t-1)}\\ &=\frac{(1+i)^t-(1+i)^{t-1}}{(1+i)^{t-1}}\\ &=\frac{(1+i)^{t-1}\times[(1+i)-1]}{(1+i)^{t-1}}\\ &=i \end{aligned} \]

其经济含义为复利条件下实际利率不会随时间t的变化而变化。

2.1.4 名义利率

在实际生活中，利率通常以年为单位，因此我们称之为年利率。但是，有时候我们会遇到一些特殊情况，比如利息的结算周期不是年，而是半年、季度、月等。这时候我们就需要将年利率转换为其他结算周期的利率，这种利率称为名义利率。

定义2.7 令\(i^{(m)}\)，表示一年结转\(m\)次的年名义利率，则每次结转利息的实际利率为\(\frac{i^{(m)}}{m}\)，年末累积值为\(\left[1+\frac{i^{(m)}}{m}\right]^m\)。

按照年名义利率\(i^{(m)}\)积累一年后的本息和为\(\left[1+\frac{i^{(m)}}{m}\right]^m\)，应该与年实际利率\(i\)积累一年后的本息和相等，即：

\[\begin{equation} \left[1+\frac{i^{(m)}}{m}\right]^m=1+i \tag{2.7} \end{equation}\]

显然，名义利率\(i^{(m)}\)与实际利率\(i\)之间的关系还可以表示为：

\[ i^{(m)}=m\times\left[\left(1+i\right)^{\frac{1}{m}}-1\right] \]

例2.6 假设你是一名银行理财经理，现在有款短期理财产品月月盈，基本情况如下：

  • 产品按月付息，年化收益率为12%，投资期限至少一个月；
  • 无本金要求，1分钱也可以投。

现在你有本金1000元，计划投资2年6个月，请计算你可以得到的累积值。

此题至少有两种解法：

一是将年名义利率转化为年实际利率9，然后计算累积值。

\[ i=\left(1+\frac{12\%}{12}\right)^{12}-1\approx 12.68\%\\ \text{累积值=}1000\times\left(1+12.68\%\right)^{2.5}\approx 1347.77 \]

二是直接利用年名义利率计算月实际利率，然后求累积值。

\[ \text{累积值}=1000 \times \left(1+\frac{12\%}{12}\right)^{12\times 2.5} \approx 1347.77 \]

2.1.5 利息力

例2.7 单位年度内实际利率为6%，请分别计算每年、每半年、每季度、每月、每半月、每天结转1次（即m=1,2,4,12,24,365）的年名义利率。

我们可以用R语言代码计算，结果如下：

#library(lifecontingencies, quietly=TRUE)
m <- c(1,2,4,12,24,365)#一年计息m次
i <- 0.06#实际利率
im<-c()#年名义利率

#使用'effective2Convertible'函数计算年名义利率
for (j in m){
  ans<-effective2Convertible(i,k=j)
  im<-c(im,ans)
}
df<-data.frame(m,im)#创建数据框

#绘制图形
plot(m,im,type="o",col="red",xlab="一年计息m次",ylab="年名义利率im")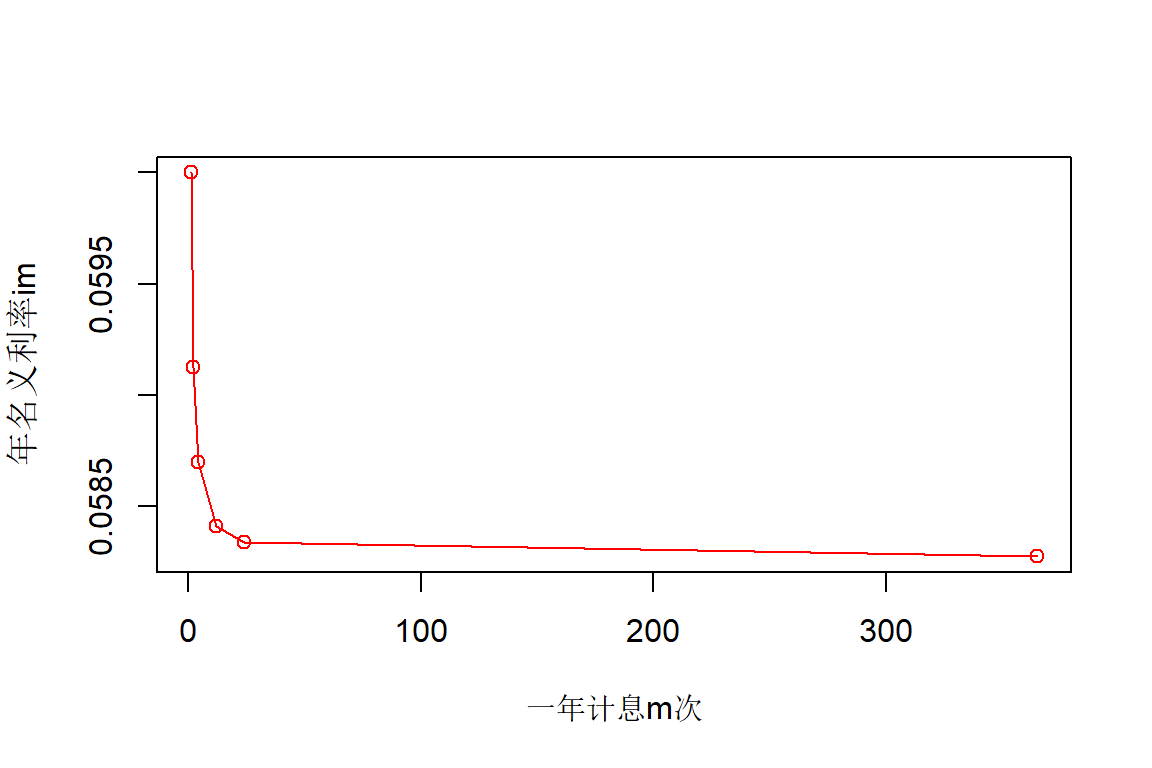
一年计息m次的年名义利率

图2.1: 一年计息m次的年名义利率 

#添加图表
knitr::kable(df,caption="一年计息m次的年名义利率")
表2.1: 一年计息m次的年名义利率
m im
1 0.0600000
2 0.0591260
4 0.0586954
12 0.0584106
24 0.0583397
365 0.0582736

从图中可以看出，当年实际利率大于零且保持一定的条件下，随着计息次数的增加，年名义利率越来越趋近于一个值。特别是在复利条件下，当计息次数趋近于无穷大，年名义利率与年实际利率的关系为

\[\begin{equation} \delta_t=\lim_{m\to\infty}i^{(m)}=\lim_{m\to\infty}m\times\left[\left(1+i\right)^{\frac{1}{m}}-1\right]=\ln(1+i) \tag{2.8} \end{equation}\]

为了更一般地描述累积过程中的瞬时年化利率，我们引入利息力的概念。

定义2.8 利息力（interest force），又称“息力”、“利息强度”， 是衡量确切时点上利率水平的指标，记作\(\delta_t\)。

\[\begin{equation} \begin{split} \delta_t&=\lim_{\Delta t \to 0} \frac{a(t+\Delta t)-a(t)}{a(t)\times \Delta t}\\ &=\frac{a'(t)}{a(t)} \\ &=\left[\ln a(t)\right]' \end{split} \tag{2.9} \end{equation}\]

根据式(2.9)，我们可以得到关于利息力\(\delta_t\)的\(a(t)\)表达式

\[\begin{equation} a(t)=e^{\int_0^t\delta_sds}\tag{2.10} \end{equation}\]

2.1.6 复利条件下不同利率之间的关系

在复利条件下，实际利率、实际贴现率、贴现因子以及利息力之间是可以相互转换计算的，结果如2.2所示：

复利条件下不同利率之间的关系

图2.2: 复利条件下不同利率之间的关系

2.2 确定性年金

2.2.1 年金分类

定义2.9 年金（Annuity）是指一系列有规律的现金流。

年金最原始的涵义是指一年付款一次，每次支付相等金额的一系列款项。但现在，年金的涵义已经得到了推广，它被广泛应用于更加一般的情形，如每季度、每月或每周付款一次的一系列付款都被看作是年金。此外，每次付款的金额也未必是相等的，它完全可以按照某种规律递增或递减。

年金存在各种各样的形式。按照不同的标准，可以将这些年金划分为不同的类型。

  • 按照年金的支付时间和支付金额是否确定，年金可以划分为确定性年金和风险年金。如果年金的支付时间和支付金额都是事先确定的，那么这种年金就是确定性年金。如某公司发行的附息债券，每年支付的利息金额就是一种确定性年金。为简单起见，后面将确定性年金直接称作年金，这也是本节讨论的对象。支付时间和支付金额并不确定的年金被称作风险年金，特别是年金支付取决于被保险人的生存状态时，此类产品通常被称为生命年金。如终身生存年金就是一种典型的生命年金，从年金开始给付一直到被保险人死亡的整个期间，保险公司都得定期给付年金，但被保险人何时死亡是不确定的，因此年金的给付时间和给付金额都是不确定的，它取决于被保险人的寿命。

  • 按照年金的支付期限长短，年金可以划分为定期年金和永续年金。年金的支付期限是指从第一次付款开始直至最后一次付款结束的整个期间。如果年金的支付期限是有限的，那么相应的年金被称作定期年金；如果年金的支付期限是无限的，那么相应的年金被称作永续年金（ Perpetuity 或Perpetual Annuity）。西方有些债券是无期限债券，这些债券的利息可视为永续年金。此外，优先股因为有固定的股息而又无到期日，所以优先股股息有时也可以看作是永续年金。

  • 按照年金的支付周期不同，年金可以分为每年支付一次的年金，每季支付一次的年金，每月支付一次的年金等。如果年金是连续不断地支付，那么这种年金被称作连续年金。

  • 按照年金在每期的支付时点不同，年金可以分为期初付年金（Annuity Due 或 Annuity in Advance）和期末付年金（Annuity Immediate 或 Annuity in Arrears）。期初付年金是指在每个支付周期初（如年初、季初、月初等）支付的年金，期末付年金是指在每个支付周期末（如年末、季末、月末等）支付的年金。

  • 按照年金开始支付的时间不同，年金可以分为即期年金和延期年金（Deferred Annuity）。即期年金是指立即开始支付的年金。延期年金是指经过一定时期以后才开始支付的年金。

  • 按照每次付款的金额是否相等，年金可以划分为等额年金和变额年金。等额年金是指每次支付相等金额的年金。变额年金是指各次付款金额并不相等的年金。如果没有特别说明，本书中的“年金”均指等额年金。

2.2.2 年金现值

定义2.10 年金现值（Present Value of Annuity）是指一系列付款折现到期初的价值。

  1. 期末付年金现值

假设年金支付期限是n个时期，在每个时期末支付1元，这种年金就是期末付定期年金。其现值一般用符号\(a_{\overline{n}|i}\)表示，其中n表示年金的支付期限，i表示计算年金现值的利率，在不致引起混淆的情况下，通常简记为\(a_{\overline{n}|}\)，其计算过程如下图所示。

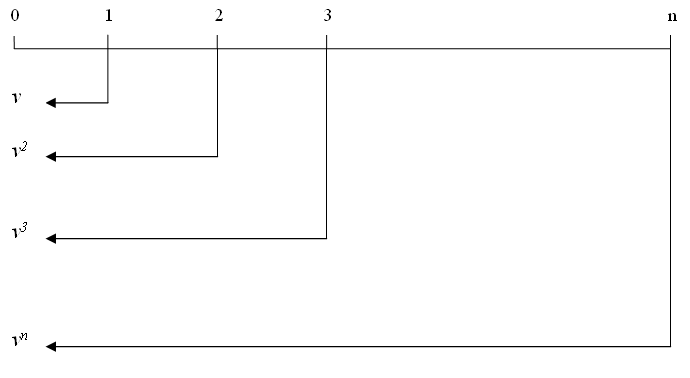
期末付定期年金现值

图2.3: 期末付定期年金现值

期末付定期年金的现值计算公式为：

\[\begin{equation} \begin{split} a_{\overline{n}|}&=v+v^2+v^3+\dots + v^{n-1}+v^{n}\\ &=\sum_{t=1}^{n}v^{t}\\ &=\frac{1-v^n}{i} \end{split} \tag{2.11} \end{equation}\]

例2.8 客户希望在未来5年里，每年末向一个偏债基金投资10000元，期望年实际利率为5%。计算上述投资的现值。

解：

本金为10000元，年实际利率为5%，投资期限为5年。将上述参数带入期末付年金现值公式(2.11)得

\[ \begin{aligned} \text{现值}&=10000\times a_{\overline{n}|}\\ &=10000 \times \frac{1-v^n}{i}\\ &=10000 \times \frac{1-(1+5\%)^{-5}}{5\%}\\ &\approx 43294.77 \end{aligned} \]

也可以直接利用R实现

n<-5#期限
ir<-0.05#年利率
(an<-10000*annuity(ir,n,m=0,k=1,type="immediate"))#immediate的意思是期末付，m是延后年数，k是一年计息次数
## [1] 43294.77
  1. 期初付年金现值

假设年金支付期限是n个时期，在每个时期初支付1元，这种年金就是期初付定期年金。其现值一般用符号\(\ddot a_{\overline{n}|i}\)表示，其中n表示年金的支付期限，i表示计算年金现值的利率。与期末付年金类似，通常简记为\(\ddot a_{\overline{n}|}\)，其计算过程如下图所示。

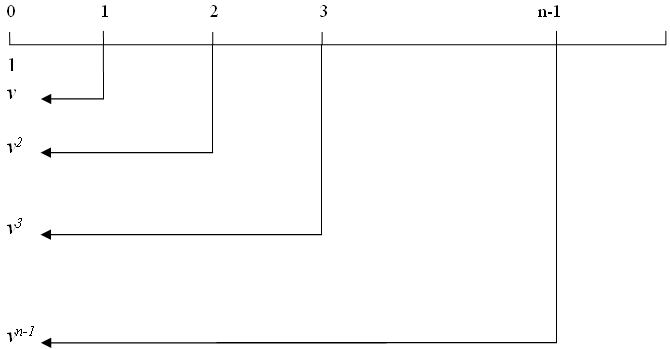
期初付定期年金现值

图2.4: 期初付定期年金现值

期初付定期年金的现值计算公式为：

\[\begin{equation} \begin{split} \ddot a_{\overline{n}|}&=1+v+v^2+v^3+\dots + v^{n-2}+v^{n-1}\\ &=\sum_{t=0}^{n-1}v^{t}\\ &=\frac{1-v^n}{d} \end{split} \tag{2.12} \end{equation}\]

例2.9 某企业租用了一间仓库，一次性支付50000元的租金后可以使用8年。假设年实际利率为6%，试计算如果每年初支付租金，该仓库的年租金应该是多少？

解：设每年初的租金为A，则根据题意，可以建立下述方程

\[A\times \ddot a_{\overline{n}|}=50000\] 将年实际利率（i=6%）、出租年限（n=8年）带入上式并整理得

\[ \begin{aligned} A&=\frac{50000}{\ddot a_{\overline{n}|}}\\ &=\frac{50000}{\frac{1-(1+6\%)^{-8}}{\frac{6\%}{1+6\%}}}\\ &\approx 7596.04 \end{aligned} \]

利用R可得

n<-8#期限
ir<-0.06#年利率
50000/annuity(ir,n,m=0,k=1,type="due")#due表示期初付
## [1] 7596.035
  1. 一年内多次收付的年金现值

定义2.11 每年收付\(m\)次、每次\(\frac{1}{m}\)元的期末付年金现值记为\(a_{\overline{n}|}^{(m)}\)

每年收付\(m\)次、每次\(\frac{1}{m}\)元的期初付年金现值记为\(\ddot a_{\overline{n}|}^{(m)}\)

一年内多次收付的期末付和期初付年金现值计算公式分别为：

\[\begin{equation} a_{\overline{n}|}^{(m)}=\frac{1-v^n}{i^{(m)}} \tag{2.13} \end{equation}\]

\[\begin{equation} \ddot a_{\overline{n}|}^{(m)}=\frac{1-v^n}{d^{(m)}} \tag{2.14} \end{equation}\]

例2.10 某企业租用了一处仓库，一次性支付50000元的租金后可以使用8年。假设每年计息四次的年名义利率为8%，试计算如果每季度初支付租金，该仓库的季度租金应该是多少？

解法1：设每个季度为一个计息周期，租赁期共有\((8\times 4=32)\)个季度，并且季度实际利率为\(\frac{8\%}{4}=2\%\)

根据题意，可以建立下述方程

\[ A\times \ddot a_{\overline{n\times k}|{i=2\%}}=50000 \]

其中：n为租赁期限，k为计息次数，A为季度初付租金。

显然，季度实际利率为\(\frac{8\%}{4}=2\%\)，季度实际贴现率为\(\frac{2\%}{1+2\%}\approx 1.96\%\)

将季度实际利率（2%）、季度实际贴现率（1.96%）、出租季度数（32）带入上式并整理得

\[ \begin{aligned} A&=\frac{50000}{\ddot a_{\overline{n\times k}|{i=2\%}}}\\ &=\frac{50000}{\frac{1-(1+2\%)^{-32}}{1.96\%}}\\ &\approx \frac{50000}{23.95}\\ &\approx 2087.68 \end{aligned} \]

解法2：设每季度初的租金为A，则根据题意，可以建立下述方程

\[ (4\times A)\times \ddot a_{\overline{n}|}^{(4)}=50000 \]

即： \[ \begin{aligned} 4\times A&=\frac{50000}{\ddot a_{\overline{n}|}^{(4)}}\\ &=\frac{50000}{\frac{1-(1+i)^{-n}}{d^{(m)}}} \end{aligned} \]

首先，根据(2.7)进行年名义利率和年实际利率的换算，得：

\[ \begin{aligned} \because 1+i&=\left[1+\frac{i^{(4)}}{4}\right]^4\\ \therefore i&=\left[1+\frac{i^{(4)}}{4}\right]^4-1\\ &=(1+\frac{8\%}{4})^4-1\\ &\approx 8.24\% \end{aligned} \]

其次，根据(2.3)进行年实际利率和年实际贴现率的换算，得：

\[ \begin{aligned} d&=\frac{i}{1+i}\\ &=\frac{8.24\%}{1+8.24\%}\\ &\approx 7.61\% \end{aligned} \]

再次，根据年实际贴现率和年名义贴现率的换算公式

\[1-d=\left[1-\frac{d^{(m)}}{m}\right]^m\]

可得：

\[ \begin{aligned} d^{(m)}&=\left[1-(1-d)^{\frac{1}{m}}\right]\times m\\ &=\left[1-(1-7.61\%)^{\frac{1}{4}}\right]\times 4\\ &\approx 7.84\% \end{aligned} \]

最后，将年实际利率（i=8.24%）、年名义贴现率（\(d^{(4)}\)=7.84%）、出租年限（n=8年）带入(2.14)得

\[ \begin{aligned} \ddot a_{\overline{n}|}^{(4)}&=\frac{1-(1+i)^{-n}}{d^{(m)}}\\ &=\frac{1-(1+8.24\%)^{-8}}{7.84\%}\\ &\approx 5.99 \end{aligned} \]

显然，季度初付租金为：

\[ \begin{aligned} A&=\frac{50000}{5.99}\div 4\\ &\approx 2086.81 \end{aligned} \]

利用R可得:

n<-8#期限
im<-0.08#年名义利率
k<-4#一年计息次数

###解法1
ir.season<-im/k#季度实际利率
a.due.season<-annuity(ir.season,n*k,type="due")#计算期初付年金现值，due表示期初付
rent1<-50000/a.due.season#计算季度租金
print(paste("第一种方法计算的季度租金为：",round(rent1,5)))
## [1] "第一种方法计算的季度租金为： 2088.75526"
###解法2：直接使用annuity函数计算
ir<-convertible2Effective(im,k)#计算年实际利率
a.due.year<-annuity(ir,n,k=4,type="due")#计算期初付年金现值，due表示期初付
rent2<-50000/a.due.year/k#计算年租金
print(paste("第一种方法计算的年租金为：",round(rent2,5)))
## [1] "第一种方法计算的年租金为： 2088.75526"

2.2.3 年金终值

定义2.12 年金终值（Future Value of Annuity）是指一系列付款累积到期末的价值。

与年金现值类似，年金终值也可以分为期末付年金终值和期初付年金终值，主要分类及其计算公式为：

  • 期末付年金终值记为\(s_{\overline{n}|}\)

\[\begin{equation} s_{\overline{n}|}=\frac{(1+i)^n - 1}{i} \tag{2.15} \end{equation}\]

  • 期初付年金终值记为\(\ddot s_{\overline{n}|}\)

\[\begin{equation} \ddot{s}_{\overline{n}|}=\frac{(1+i)^n - 1}{d} \tag{2.16} \end{equation}\]

  • 一年内多次收付的期末付年金终值记为\(s_{\overline{n}|}^{(m)}\)

\[\begin{equation} s_{\overline{n}|}^{(m)}=\frac{(1+i)^n - 1}{i^{(m)}} \tag{2.17} \end{equation}\]

  • 一年内多次收付的期初付年金终值记为\(\ddot s_{\overline{n}|}^{(m)}\)

\[\begin{equation} \ddot{s}_{\overline{n}|}^{(m)}=\frac{(1+i)^n - 1}{d^{(m)}} \tag{2.18} \end{equation}\]

例2.11 张三在30岁时开始每年初向一个偏债基金投资10000元，期望年实际利率为5%。

  1. 试计算张三在65岁退休时可以得到的累积值。
  2. 如果张三在退休时将投资转为每年初支付的确定年金，该年金在退休后20年内每年末领取一次，试计算张三每年可领取的金额。

解：

  1. 张三在65岁退休时可以得到的累积值为

\[ \begin{aligned} \text{累积值}&=10000\times s_{\overline{35}|}\\ &=10000\times \frac{(1+5\%)^{35} - 1}{\frac{5\%}{1+5\%}}\\ &\approx 10000\times 94.84\\ &\approx 948400 \end{aligned} \]

利用R可得：

n<-35#期限
ir<-0.05#年利率
10000*accumulatedValue(ir,n,m=0,k=1,type="due")#due的意思是期初付，m是延后年数，k是一年计息次数
## [1] 948363.2
  1. 如果张三在退休时将投资转为每年初支付的确定年金，该年金在退休后20年内每年末领取一次，令每年领取的金额为A，则根据题意得：

\[ \because A\times a_{\overline{20}|}=948400\\ \begin{aligned} \therefore A&=\frac{948400}{a_{\overline{20}|}}\\ &=\frac{948400}{\frac{1-(1+5\%)^{-20}}{5\%}}\\ &\approx 948400/12.46\\ &\approx 76102.07 \end{aligned} \]

利用R可得：

n<-20#期限
ir<-0.05#年利率
948400/annuity(ir,n,m=0,k=1,type="immediate")#immediate的意思是期末付，m是延后年数，k是一年计息次数
## [1] 76102.07

2.3 无风险收益证券及其利率风险度量

2.3.1 无风险收益证券定价

定义2.13 无风险收益证券是指没有违约风险的债券，即债券发行人有足够的偿付能力，能够按照约定的时间和金额支付利息和本金。

既然无风险收益证券没有违约风险，其现金流就是确定无疑的，即无风险收益证券的现值应该等于未来的现金流的现值。因此无风险收益证券的产品参数为：

  • 票面价值（确定）：\(F\)
  • 票面利率（确定）：\(r\)
  • 发行期限（确定）：\(n\)
  • 一年计息次数（确定）：\(m\)
  • 付息时间（确定）：\(\text{期末}\)
  • 市场无风险利率（不确定）：\(i\)
  • 发行价格（不确定）：\(P\)

显然，无风险收益证券的价格P是由市场无风险利率i决定的，无风险收益证券定价公式为：

\[\begin{equation} \begin{split} P&=P(i)\\ &=\sum_{t=1}^{n}F\times r \times v^t+F\times v^n\\ &=F\times r \times a_{\overline{n}|}^{(m)}+F\times v^n \end{split} \tag{2.19} \end{equation}\]

2.3.2 久期和凸性

由于无风险收益证券的价格只受到市场无风险利率的影响，因此我们可以通过久期和凸性来度量无风险收益证券的利率风险。

定义2.14 久期（Duration）是一种衡量债券价格对利率变动的敏感性的指标，当市场无风险利率变动\(\Delta i\)时，证券价格随之变动的幅度，即

\[\begin{equation} \begin{split} D&=\frac{\left|\frac{\Delta P}{P}\right|}{\Delta i}\\ &=-\frac{1}{P}\times \frac{\Delta P}{\Delta i} \end{split} \tag{2.20} \end{equation}\]

根据久期计算公式(2.20)，将(2.19)带入得： \[ \begin{aligned} \because \frac{dP}{di}&=-\left(\sum^n_{t=1} Frtv^{t+1}+Fnv^{n+1}\right)<0\\ \newline \therefore \frac{dP}{P}&=-\frac{\sum^n_{t=1} Frtv^{t+1}+Fnv^{n+1}}{P}di\\ &=-\left(\sum^n_{t=1} \underbrace{\frac{Frv^{t+1}}{P}}_{(1)}\times t + \underbrace{\frac{Fv^{n+1}}{P}}_{(2)}\times n\right)di\\ \newline \therefore D&=\sum^n_{t=1} \frac{Frv^{t+1}}{P}\times t + \frac{Fv^{n+1}}{P}\times n\\ \end{aligned} \]

仔细观察上式中的(1)与(2)的和为无风险收益证券的价格P，从经济含义上久期是证券付息年份的加权平均，这也是久期这个定义的由来。

凸性convexity：

根据泰勒展开式10，我们可以得到无风险收益证券的价格变动量\(\Delta P\)与市场无风险利率变动量\(\Delta i\)之间的关系：

\[ P(i+\Delta i)\approx P(i)+\frac{dP}{di}\Delta i+\frac{1}{2}\frac{d^2P}{di^2}(\Delta i)^2 \]

因此，无风险收益证券的凸性计算公式为：

\[C=\frac{1}{P}\times \frac{d^2P}{di^2}\]

其中：

\[\frac{d^2P}{di^2}=\sum^n_{t=1} Frt(t+1)v^{t+2}+Fn(n+1)v^{n+2}>0\]

例2.12 某公司发行了一只票面价值为1000元、票面利率为5%、期限为5年、每年末付息的无风险收益证券。目前市场无风险利率为4%，试计算该无风险收益证券的久期和凸性。

解：

利用R计算：

F<-1000#票面价值
r<-0.05#票面利率
n<-5#期限
iff<-0.04#市场无风险利率

cashflows<-c(rep(F*r,n),1000)#现金流
timeids<-c(1:n,n)#现金流对应的时间

D<-duration(cashFlows=cashflows,timeIds=timeids,i=iff,k=1,macaulay=TRUE)#计算久期
C<-convexity(cashFlows=cashflows,timeIds=timeids,i=iff,k=1)#计算凸性

print(paste("该无风险收益证券的久期为：",round(D,5)))
## [1] "该无风险收益证券的久期为： 4.55709"
print(paste("该无风险收益证券的凸性为：",round(C,5)))
## [1] "该无风险收益证券的凸性为： 24.47657"

2.4 课后习题

  1. 已知\(A(t)=2t+\sqrt{t}+5\)，求

    • 对应的\(a(t)\)
    • \(I_3\)
    • \(i_4\)

  2. 若\(i_k\)是时期k的单利利率（k=1,2,3,…,n），证明：\(a(n)-a(0)=i_1+i_2+...+i_k\)

  3. 在不同的复利利率条件下，计算本金翻倍所需要的连续投资年数:2%、3%、5%、8%、10%

  4. 设利息力为5%，时刻0的初始资金为1，计算半年、3.5年以后的累积值。

  5. 基金A以每月计息一次的年名义利率12%积累，基金B以利息力\(\delta_t=\frac{t}{6}\)积累。在时刻0，两笔基金存入相同的金额后，试确定两个基金金额相等的下一个时刻。

  6. 试证明\(\frac{d^3}{(1-d)^2}=\frac{(i-d)^2}{1-v}\)，其中\(i\)为利率，\(d\)为贴现率，\(v\)为折现因子。

  7. 证明(\(n\geq m\))：\(v^n-v^m=i(a_{\overline{m}|}-a_{\overline{n}|})\)

  8. 张三通过分期付款方式购买了一辆现价为20万元的家用汽车，如果他首期支付一笔款项后，在今后的5年内每月末付款3093.25元即可付清车款。假设该笔贷款使用每月结转一次利息的年名义利率为6%，试计算A的首期付款金额是多少。

  9. 张三通过基金定投方式储备养老金。已知张三从25周岁开始，每月末固定向偏债型基金投资1000元，期望年实际利率为5%，试计算张三在65岁时可以得到的累积值。

  10. 试计算永续国债的市场价格及其久期和凸性，其中无风险市场利率为\(i\)。

  1. 年名义利率与年实际利率之间的换算，参见 baoxianke.top ，这个网站是我自己鼓捣的，不一定稳定哈:-)↩︎

  2. 泰勒公式的基本思想是，如果一个函数在某一点处足够光滑（即具有足够高的连续导数），那么该函数在该点附近可以用一个多项式来近似表示，即\(f(x)=\sum_{k= 0}^{n}\frac{f^{(k)}(x_0)}{k!}(x-x_0)^{k}+R_{n}(x_0)\)。↩︎